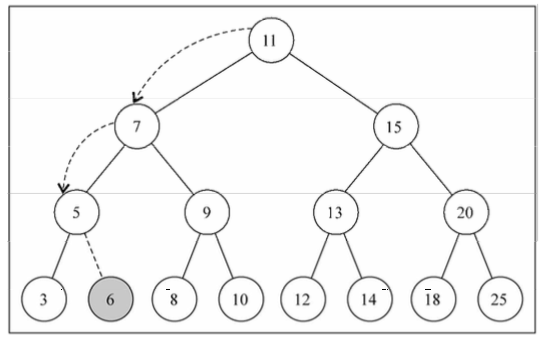
1 树

一个树结构包含一系列存在父子关系的节点。每个节点都有一个父节点(除了顶部的第一个节点)以及零个或多个子节点。位于树顶部的节点叫作根节点(11)。它没有父节点。树中的每个元素都叫作节点,节点分为内部节点和外部节点。至少有一个子节点的节点称为内部节点。没有子元素的节点称为外部节点或叶节点。节点的一个属性是深度,节点的深度取决于它的祖先节点的数量。树的高度取决于所有节点深度的最大值。一棵树也可以被分解成层级。根节点在第0层,它的子节点在第1层,以此类推。

1.1 二叉树和二叉搜索树

二叉树中的节点最多只能有两个子节点:一个是左侧子节点,另一个是右侧子节点。这些定义有助于我们写出更高效的向树中插入、查找和删除节点的算法。

对于二叉搜索树，我们一般需要实现如下方法：

insert(key): 向书中插入一个新的键。
search(key): 在树中查找一个键，如果节点存在，则返回true，否则返回false。
inOrderTraverse: 通过中序遍历方式遍历所有节点。
preOrderTraverse: 通过先序遍历方式遍历所有节点。
postOrderTraverse: 通过后序遍历方式遍历所有节点。
min: 返回树中最小的键/值。
max: 返回树中最大的健/值。
remove(key): 从树中移除某个键。

1.1.1 二叉搜索树的遍历

二叉搜索树(BST)是二叉树的一种,但是它只允许你在左侧节点存储(比父节点)小的值, 在右侧节点存储(比父节点)大(或者等于)的值。

中序遍历是一种以上行顺序访问BST所有节点的遍历方式,也就是以从最小到最大的顺序访问所有节点。中序遍历的一种应用就是对树进行排序操作。

先序遍历是以优先于后代节点的顺序访问每个节点的。先序遍历的一种应用是打印一个结构化的文档。先序遍历和中序遍历的不同点是,先序遍历会先访问节点本身,然后再访问它的左侧子节点，最后是右侧子节点。

后序遍历则是先访问节点的后代节点,再访问节点本身。后序遍历的一种应用是计算一个目录和它的子目录中所有文件所占空间的大小。

树中有三种经常执行的搜索类型，最小值，最大值，搜索特定的值。

1.1.2 二叉搜索树的实现与基本使用

下面的minNode方法允许我们从树中任意一个节点开始寻找最小的键。我们可以使用它来找到一棵树或它的子树中最小的键。因此,我们在调用minNode方法的时候传入树的根节点(行{1}), 因为我们想要找到整棵树的最小键。

可以把代码中的几个内部方法也写成二叉树结构的属性，这样可以灵活引用。这里我们就不具体修改了。

function BinarySearchTree() {
    function Node(key) {
        this.key = key;
        this.left = null;
        this.right = null;
    }
    this.root = null;

    if ((typeof this.insert !== 'function') && (typeof this.insert !== 'string')) {
        //内部私有方法，用于插入节点
        function insertNode(node, newNode) {
            if (node.key > newNode.key) {
                if (node.left === null) {
                    node.left = newNode;
                } else {
                    insertNode(node.left, newNode);
                }
            } else {
                if (node.right === null) {
                    node.right = newNode;
                } else {
                    insertNode(node.right, newNode);
                }
            }
        }
        BinarySearchTree.prototype.insert = function(key) {
            var newNode = new Node(key);
            if (this.root === null) {
                this.root = newNode;
            } else {
                insertNode(this.root, newNode);
            }
        };
        BinarySearchTree.prototype.inOrderTraverse = function(callback) {
            //中序遍历的私有方法,从小到大遍历
            function inOrderTraverseNode(node, callback) {
                if (node !== null) {
                    inOrderTraverseNode(node.left, callback);
                    callback(node.key);
                    inOrderTraverseNode(node.right, callback);
                }
            }
            inOrderTraverseNode(this.root, printNode);
        };
        BinarySearchTree.prototype.preOrderTraverse = function(callback){
            function preOrderTraverseNode(node,callback){
                if (node !== null) {
                    callback(node.key);
                    preOrderTraverseNode(node.left,callback);
                    preOrderTraverseNode(node.right,callback);
                }
            }
            preOrderTraverseNode(this.root,callback);
        };
        BinarySearchTree.prototype.postOrderTraverse = function(callback){
            function postOrderTraverseNode(node,callback){
                if (node !== null) {
                    postOrderTraverseNode(node.left,callback);
                    postOrderTraverseNode(node.right,callback);
                    callback(node.key);
                }
            }
            postOrderTraverseNode(this.root,callback);
        };
        BinarySearchTree.prototype.min = function(){
            function minNode(node){
                if (node) {
                    while(node && node.left !== null){
                        node = node.left;
                    }
                    return node.key;
                }
                return null;
            }
            //调用内部方法
            return minNode(this.root);
        };
        BinarySearchTree.prototype.max = function(){
            function maxNode(node){
                if (node) {
                    while(node && node.right !== null){
                        node = node.right;
                    }
                    return node.key;
                }
                return null;
            }
            //调用内部方法
            return maxNode(this.root);
        };
        BinarySearchTree.prototype.search = function(key){
            function searchNode(node,key){
                if (node === null) {
                    return false;
                }
                if (node.key < key) {
                    return searchNode(node.right,key);
                }else if(node.key > key){
                    return searchNode(node.left,key);
                }else{
                    return true;
                }
            }
            return searchNode(this.root,key);
        };
        BinarySearchTree.prototype.remove = function(key){
            function findMinNode(node){
                if (node) {
                    while(node && node.left !== null){
                        node = node.left;
                    }
                    return node;
                }
                return null;
            }
            function removeNode(node,key){
                if (node === null) {
                    return null;
                }
                if (key < node.key) {
                    node.left = removeNode(node.left,key);
                    return node;
                }else if(key > node.key){
                    node.right = removeNode(node.right,key);
                    return node;
                }else{//键等于node.key
                    //第一种情况，一个叶节点
                    if (node.left === null && node.right === null) {
                        node = null;
                        return node;
                    }
                    //第二种情况 一个只有一个子节点的节点
                    if (node.left === null) {
                        node = node.right;
                        return node;
                    }else if (node.right === null){
                        node = node.left;
                        return node;
                    }
                    //第三种情况 一个有两个子节点的节点
                    var aux = findMinNode(node.right);
                    node.key = aux.key;
                    node.right = removeNode(node.right,aux.key);
                    return node;
                }
            }
            this.root = removeNode(this.root,key);
        };
    }
}

二叉树基本使用：

//遍历节点操作
function printNode(value) {
    console.log(value);
}
var tree = new BinarySearchTree();
tree.insert(11);
tree.insert(7);
tree.insert(15);
tree.insert(5);
tree.insert(3);
tree.insert(9);
tree.insert(8);
tree.insert(10);
tree.insert(13);
tree.insert(12);
tree.insert(14);
tree.insert(20);
tree.insert(18);
tree.insert(25);
tree.insert(6);
//中序遍历
tree.inOrderTraverse(printNode);//3 5 6 7 8 9 10 11 12 13 14 15 18 20 25
//先序遍历
tree.preOrderTraverse(printNode);//11 7 5 3 6 9 8 10 15 13 12 14 20 18 25
//后序遍历
tree.postOrderTraverse(printNode);//3 6 5 8 10 9 7 12 14 13 18 25 20 15 11
console.log(tree.min());
console.log(tree.max());
//搜索
console.log(tree.search(1) ? 'Key 1 found.' : 'Key 1 not found.');//Key 1 not found.
console.log(tree.search(8) ? 'Key 8 found.' : 'Key 8 not found.');//Key 8 found.
//移除节点
tree.remove(15);
tree.inOrderTraverse(printNode);////3 5 6 7 8 9 10 11 12 13 14 15 18 20 25
//console.log(tree.remove(100));

2 图

2.1 图的相关概念

由一条边连接在一起的顶点称为相邻顶点。一个顶点的度是其相邻顶点的数量。如果图中不存在环,则称该图是无环的。

如果图中每两个顶点间都存在路径,则该图是连通的。

图可以是无向的(边没有方向)或是有向的(有向图)。

图还可以是未加权的或是加权的。

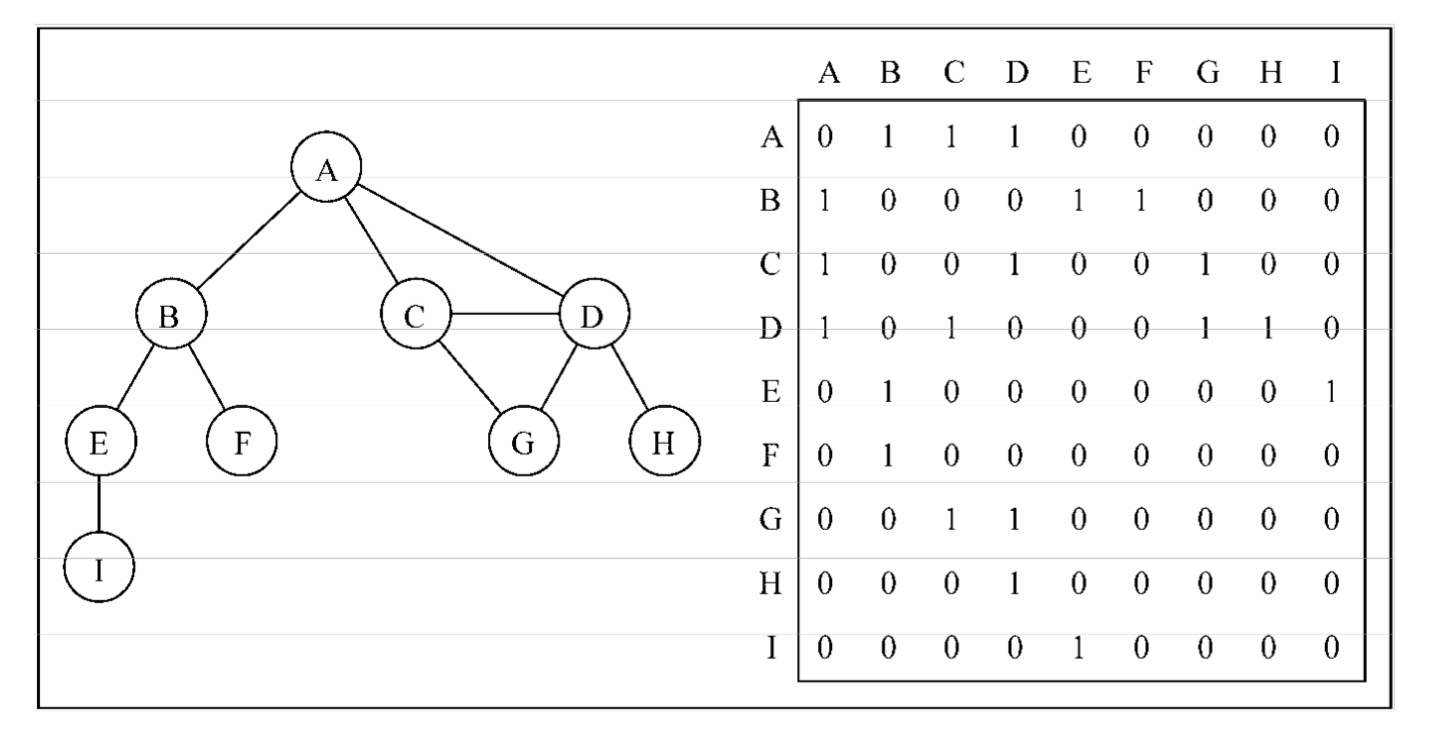
图最常见的实现是邻接矩阵。每个节点都和一个整数相关联,该整数将作为数组的索引。我们用一个二维数组来表示顶点之间的连接。如果索引为i的节点和索引为j的节点相邻,则array[i][j] === 1,否则array[i][j] === 0,邻接矩阵如下图所示:

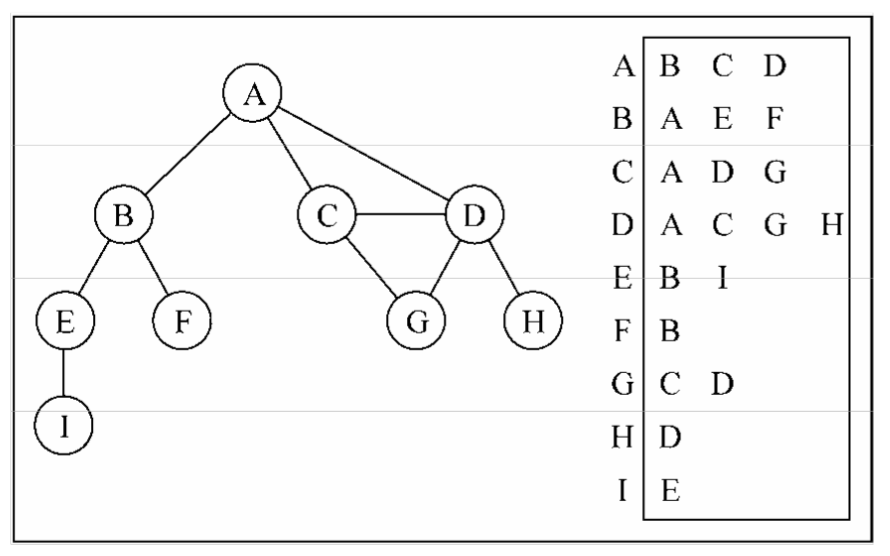
我们也可以使用一种叫作邻接表的动态数据结构来表示图。邻接表由图中每个顶点的相邻顶点列表所组成。存在好几种方式来表示这种数据结构。我们可以用列表(数组)、链表,甚至是散列表或是字典来表示相邻顶点列表。下面的示意图展示了邻接表数据结构。

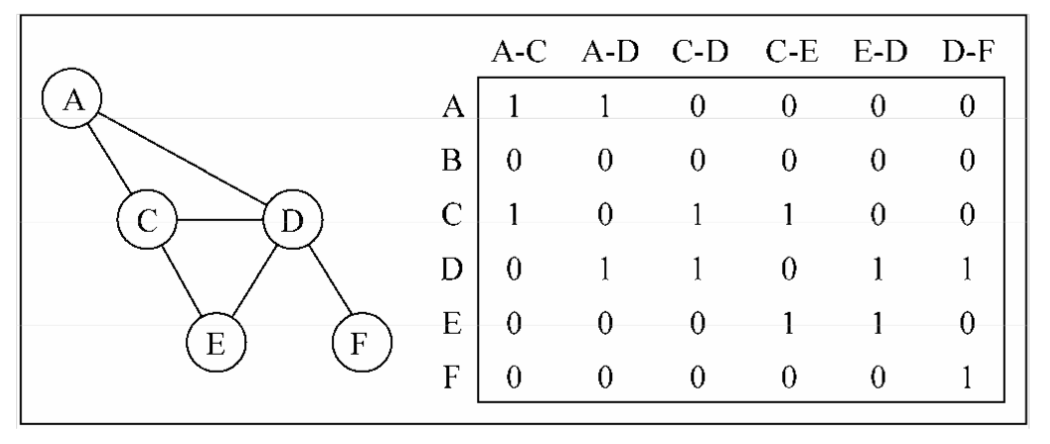
我们还可以用关联矩阵来表示图。在关联矩阵中,矩阵的行表示顶点,列表示边。如下图所示,我们使用二维数组来表示两者之间的连通性,如果顶点v是边e的入射点,则array[v][e] === 1; 否则,array[v][e]===0。关联矩阵通常用于边的数量比顶点多的情况下,以节省空间和内存。

尽管邻接表可能对大多数问题来说都是更好的选择,但以上两种表示法都很有用,且它们有着不同的性质(例如,要找出顶点v和w是否相邻,使用邻接矩阵会比较快)。在后面示例中, 我们将会使用邻接表表示法。

2.2 图的遍历

和树数据结构类似,我们可以访问图的所有节点。有两种算法可以对图进行遍历:广度优先搜索(Breadth-First Search,BFS)和深度优先搜索(Depth-First Search,DFS)。图遍历可以用来寻找特定的顶点或寻找两个顶点之间的路径,检查图是否连通,检查图是否含有环等。

图遍历算法的思想是必须追踪每个第一次访问的节点,并且追踪有哪些节点还没有被完全探索。对于两种图遍历算法,都需要明确指出第一个被访问的顶点。

完全探索一个顶点要求我们查看该顶点的每一条边。对于每一条边所连接的没有被访问过的顶点,将其标注为被发现的,并将其加进待访问顶点列表中。

为了保证算法的效率,务必访问每个顶点至多两次。连通图中每条边和顶点都会被访问到。广度优先搜索算法和深度优先搜索算法基本上是相同的,只有一点不同,那就是待访问顶点列表的数据结构。

2.3 广度优先搜索

广度优先搜索算法会从指定的第一个顶点开始遍历图,先访问其所有的相邻点,就像一次访问图的一层。换句话说,就是先宽后深地访问顶点。

广度优先搜索和深度优先搜索都需要标注被访问过的顶点。为此,我们将使用一个辅助数组color。由于当算法开始执行时,所有的顶点颜色都是白色(行{1}),所以我们可以创建一个辅助函数initializeColor,为这两个算法执行此初始化操作。

我们会用到一个队列结构。队列的实现.html)。

2.3.1广度优先搜索的基本实现

//广度优先搜索算法 v表示初始节点，callback表示回调。
Graph.prototype.bfs = function(v, callback){
    var color = initializeColor(this.vertices);
    var queue = new Queue();//存储待访问和待探索的节点
    queue.enqueue(v);
    while(!queue.isEmpty()){
        var u = queue.dequeue();
        //获取u的相邻节点列表
        var neighbors = this.adjList.get(u);
        color[u] = 'grey';
        for(var i = 0; i < neighbors.length; i++){
            var w = neighbors[i];
            //如果从没有标记过，则标记为grey，加入队列
            if (color[w] === 'white') {
                color[w] = 'grey';
                queue.enqueue(w);
            }
        }
        //所有相邻节点都被标记了，所以改为黑色
        color[u] = 'black';
        //如果对于标记过得节点有操作，通过callback操作
        if (callback) {
            callback(u);
        }
    }
};

2.3.2 广度优先实现最短路径查找

给定一个图G和源顶点v,找出对每个顶点u,u和v之间最短路径的距离。

//用BFS实现最短路径
Graph.prototype.BFS = function(v, callback) {
    var color = initializeColor(this.vertices);
    var queue = new Queue(); //存储待访问和待探索的节点
    var d = [];
    var pred = [];
    queue.enqueue(v);
    for (var i = 0; i < this.vertices.length; i++) {
        d[this.vertices[i]] = 0;
        pred[this.vertices[i]] = null;
    }
    while (!queue.isEmpty()) {
        var u = queue.dequeue();
        //获取u的相邻节点列表
        var neighbors = this.adjList.get(u);
        color[u] = 'grey';
        for (var i = 0; i < neighbors.length; i++) {
            var w = neighbors[i];
            //如果从没有标记过，则标记为grey，加入队列
            if (color[w] === 'white') {
                color[w] = 'grey';
                d[w] = d[u] + 1;
                pred[w] = u;
                queue.enqueue(w);
            }
        }
        //所有相邻节点都被标记了，所以改为黑色
        color[u] = 'black';
        //如果对于标记过得节点有操作，通过callback操作
        if (callback) {
            callback(u);
        }
    }
    return {
        distances: d,
        predecessors: pred
    }
};

2.3.3 深度优先搜索基本实现

//深度优先基本实现
Graph.prototype.dfs = function(callback) {
    var self = this;
    function dfsVisit(u, color, callback) {
        color[u] = 'grey';
        if (callback) {
            callback(u);
        }
        var neighbors = self.adjList.get(u);
        for (var i = 0; i < neighbors.length; i++) {
            var w = neighbors[i];
            if (color[w] === 'white') {
                dfsVisit(w, color, callback);
            }
        }
        color[u] = 'black';
    }
    var color = initializeColor(this.vertices);
    for (var i = 0; i < this.vertices.length; i++) {
        if (color[this.vertices[i]] === 'white') {
            dfsVisit(this.vertices[i], color, callback);
        }
    }
};

2.3.4 深度优先搜索实现拓扑排序

当我们需要编排一些任务或步骤的执行顺序时,这称为拓扑排序。

//DFS可以实现输出被访问顶点的顺序，可以用于拓扑排序实现。
Graph.prototype.DFS = function(){
    var time = 0;
    var self = this;
    function DFSVisit(u,color,d,f,p){
        //console.log('discovered ' + u);
        color[u] = 'grey';
        d[u] = ++time;
        var neighbors = self.adjList.get(u);
        for(var i = 0; i < neighbors.length; i++){
            var w = neighbors[i];
            if (color[w] === 'white') {
                p[w] = u;
                DFSVisit(w,color,d,f,p);
            }
        }
        color[u] = 'black';
        f[u] = ++time;
        //console.log('explored ' + u);
    }
    var color = initializeColor(this.vertices);
    var d = [];
    var f = [];
    var p = [];
    var time = 0;
    for(var i = 0; i < this.vertices.length; i++){
        f[this.vertices[i]] = 0;
        d[this.vertices[i]] = 0;
        p[this.vertices[i]] = null;
    }
    for(var i = 0; i< this.vertices.length; i++){
        if (color[this.vertices[i]] === 'white') {
            DFSVisit(this.vertices[i], color, d, f, p);
        }
    }
    return {
        discovery:d,
        finished:f,
        predecessors:p
    }
};

2.4 图的实现

我们会实现一个邻接表的图结构。我们使用一个数组来存储图中所有顶点的名字,以及一个字典字典实现.html)来存储邻接表字典将会使用顶点的名字作为键,邻接顶点列表作为值。vertices数组和adjList字典两者都是我们Graph类的私有属性。

function Graph() {
    this.vertices = []; //点数组
    this.adjList = new Dictionary();
    if ((typeof this.addVertex !== 'function') && (typeof this.addVertex !== 'string')) {
        //私有方法，标记节点颜色 未被访问过是white 被发现是grey 已被探索black。
        function initializeColor(vertices) {
            var color = [];
            for (var i = 0; i < vertices.length; i++) {
                color[vertices[i]] = 'white';
            }
            return color;
        }
        //添加节点
        Graph.prototype.addVertex = function(v) {
            this.vertices.push(v);
            this.adjList.set(v, []); //给节点v设置一个空数组作为值。
        };
        //添加边
        Graph.prototype.addEdge = function(v, w) {
            this.adjList.get(v).push(w); //先获取v节点对应的数组，然后把w推入数组中，这样就表示一条v到w的线
            this.adjList.get(w).push(v);
        };
        //广度优先d
        //搜索算法 v表示初始节点，callback表示回调。
        Graph.prototype.bfs = function(v, callback) {
            var color = initializeColor(this.vertices);
            var queue = new Queue(); //存储待访问和待探索的节点
            queue.enqueue(v);
            while (!queue.isEmpty()) {
                var u = queue.dequeue();
                //获取u的相邻节点列表
                var neighbors = this.adjList.get(u);
                color[u] = 'grey';
                for (var i = 0; i < neighbors.length; i++) {
                    var w = neighbors[i];
                    //如果从没有标记过，则标记为grey，加入队列
                    if (color[w] === 'white') {
                        color[w] = 'grey';
                        queue.enqueue(w);
                    }
                }
                //所有相邻节点都被标记了，所以改为黑色
                color[u] = 'black';
                //如果对于标记过得节点有操作，通过callback操作
                if (callback) {
                    callback(u);
                }
            }
        };
        //用BFS实现最短路径
        Graph.prototype.BFS = function(v, callback) {
            var color = initializeColor(this.vertices);
            var queue = new Queue(); //存储待访问和待探索的节点
            var d = [];
            var pred = [];
            queue.enqueue(v);
            for (var i = 0; i < this.vertices.length; i++) {
                d[this.vertices[i]] = 0;
                pred[this.vertices[i]] = null;
            }
            while (!queue.isEmpty()) {
                var u = queue.dequeue();
                //获取u的相邻节点列表
                var neighbors = this.adjList.get(u);
                color[u] = 'grey';
                for (var i = 0; i < neighbors.length; i++) {
                    var w = neighbors[i];
                    //如果从没有标记过，则标记为grey，加入队列
                    if (color[w] === 'white') {
                        color[w] = 'grey';
                        d[w] = d[u] + 1;
                        pred[w] = u;
                        queue.enqueue(w);
                    }
                }
                //所有相邻节点都被标记了，所以改为黑色
                color[u] = 'black';
                //如果对于标记过得节点有操作，通过callback操作
                if (callback) {
                    callback(u);
                }
            }
            return {
                distances: d,
                predecessors: pred
            }
        };
        //深度优先基本实现
        Graph.prototype.dfs = function(callback) {
            var self = this;
            function dfsVisit(u, color, callback) {
                color[u] = 'grey';
                if (callback) {
                    callback(u);
                }
                var neighbors = self.adjList.get(u);
                for (var i = 0; i < neighbors.length; i++) {
                    var w = neighbors[i];
                    if (color[w] === 'white') {
                        dfsVisit(w, color, callback);
                    }
                }
                color[u] = 'black';
            }
            var color = initializeColor(this.vertices);
            for (var i = 0; i < this.vertices.length; i++) {
                if (color[this.vertices[i]] === 'white') {
                    dfsVisit(this.vertices[i], color, callback);
                }
            }
        };
        //DFS可以实现输出被访问顶点的顺序
        Graph.prototype.DFS = function(){
            var time = 0;
            var self = this;
            function DFSVisit(u,color,d,f,p){
                //console.log('discovered ' + u);
                color[u] = 'grey';
                d[u] = ++time;
                var neighbors = self.adjList.get(u);
                for(var i = 0; i < neighbors.length; i++){
                    var w = neighbors[i];
                    if (color[w] === 'white') {
                        p[w] = u;
                        DFSVisit(w,color,d,f,p);
                    }
                }
                color[u] = 'black';
                f[u] = ++time;
                //console.log('explored ' + u);
            }
            var color = initializeColor(this.vertices);
            var d = [];
            var f = [];
            var p = [];
            var time = 0;
            for(var i = 0; i < this.vertices.length; i++){
                f[this.vertices[i]] = 0;
                d[this.vertices[i]] = 0;
                p[this.vertices[i]] = null;
            }
            for(var i = 0; i< this.vertices.length; i++){
                if (color[this.vertices[i]] === 'white') {
                    DFSVisit(this.vertices[i], color, d, f, p);
                }
            }
            return {
                discovery:d,
                finished:f,
                predecessors:p
            }
        };
        Graph.prototype.toString = function() {
            var s = '';
            for (var i = 0; i < this.vertices.length; i++) {
                s += this.vertices[i] + ' -> ';
                var neighbors = this.adjList.get(this.vertices[i]);
                for (var j = 0; j < neighbors.length; j++) {
                    s += neighbors[j] + ' ';
                }
                s += ',';
            }
            return s;
        };
    }
}

2.5 图的基本使用

var graph = new Graph();
var myVertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I'];
//添加点
for (var i = 0; i < myVertices.length; i++) {
    graph.addVertex(myVertices[i]);
}
//添加点之间的关系
graph.addEdge('A', 'B');
graph.addEdge('A', 'C');
graph.addEdge('A', 'D');
graph.addEdge('C', 'D');
graph.addEdge('C', 'G');
graph.addEdge('D', 'G');
graph.addEdge('D', 'H');
graph.addEdge('B', 'E');
graph.addEdge('B', 'F');
graph.addEdge('E', 'I');
//console.log(graph.toString());//A -> B C D ,B -> A E F ,C -> A D G ,D -> A C G H ,E -> B I ,F -> B ,G -> C D ,H -> D ,I -> E 
function printNode(value) {
    console.log('Visited vertex: ' + value);
}

//广度搜索算法
//graph.bfs(myVertices[0],printNode);
//上行输出结果，节点的访问顺序
// Visited vertex: A
// Visited vertex: B
// Visited vertex: C
// Visited vertex: D
// Visited vertex: E
// Visited vertex: F
// Visited vertex: G
// Visited vertex: H
// Visited vertex: I

//广度优先搜索的使用:最短路径算法
var shortestPathA = graph.BFS(myVertices[0]);
//console.log(shortestPathA);
//上行输出结果：
// { distances: [ A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2, I: 3 ],
//   predecessors: 
//    [ A: null,
//      B: 'A',
//      C: 'A',
//      D: 'A',
//      E: 'B',
//      F: 'B',
//      G: 'C',
//      H: 'D',
//      I: 'E' ]

//深入优先搜索算法
//graph.dfs(printNode);
//上一行运行结果，节点的访问顺序
// Visited vertex: A
// Visited vertex: B
// Visited vertex: E
// Visited vertex: I
// Visited vertex: F
// Visited vertex: C
// Visited vertex: D
// Visited vertex: G
// Visited vertex: H

//深度优先搜索查找访问过程：
graph = new Graph();
myVertices = ['A','B','C','D','E','F'];
for (i=0; i<myVertices.length; i++){
    graph.addVertex(myVertices[i]);
}
graph.addEdge('A', 'C');
graph.addEdge('A', 'D');
graph.addEdge('B', 'D');
graph.addEdge('B', 'E');
graph.addEdge('C', 'F');
graph.addEdge('F', 'E');
var result = graph.DFS();
// 上面运行输出：
// discovered A
// discovered C
// discovered F
// discovered E
// discovered B
// discovered D
// explored D
// explored B
// explored E
// explored F
// explored C
// explored A

源码地址

Javascript的数据结构与算法(三)源码

...

00:00

1 树